Representing graphs in Computer Memory.
Representing data structure in memory is an interesting concept that perhaps a handful of developers haven't come across yet. Those who have done competitive programming have come across it.
The three popular ways to represent graphs in memory are:
Adjacency matrix.
Adjacency List.
Edge List.
The choice of representing the graph in memory is extremely important, therefore, picking the wrong one can result in higher space and time complexity.
Below is an in-depth analysis of the three types.
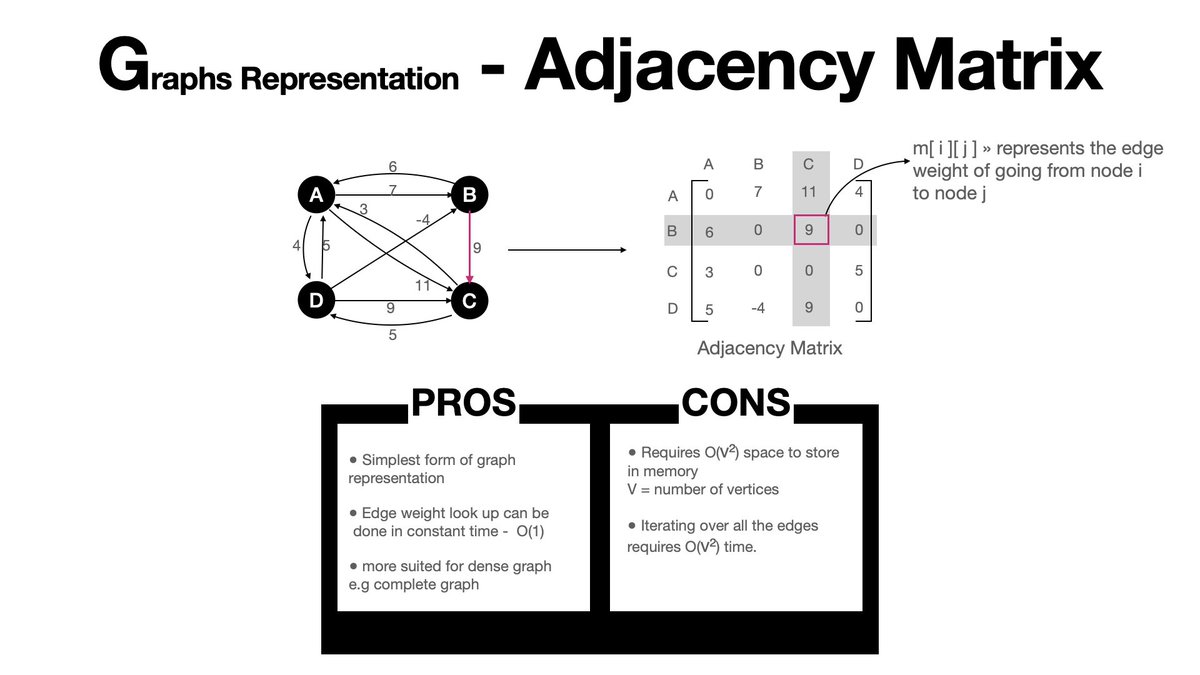
- Adjacency Matrix.
In this, the graph is represented using a 2D matrix of nxn, where n is the number of nodes in the graph. The idea is that the cell m[i][j] represents the edge weight of going from node i to j.
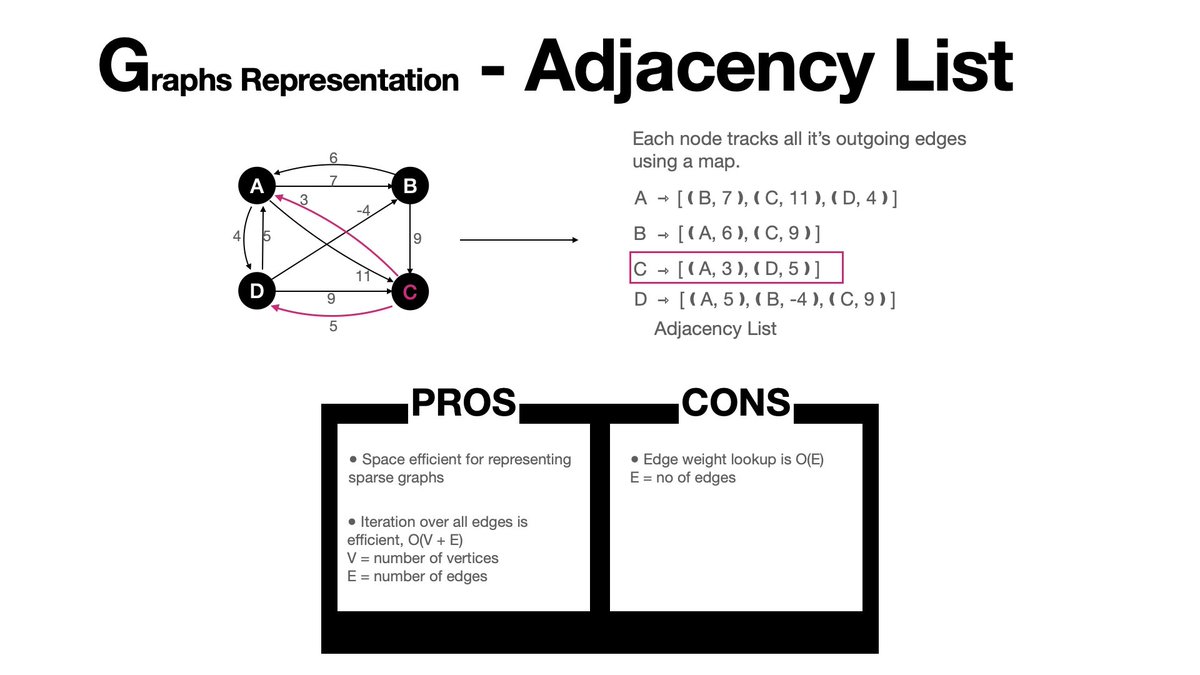
- Adjacency List.
The idea here is to represent the graph as a map, where the key is the nodes of the graph, and the value is the list of all its edges.
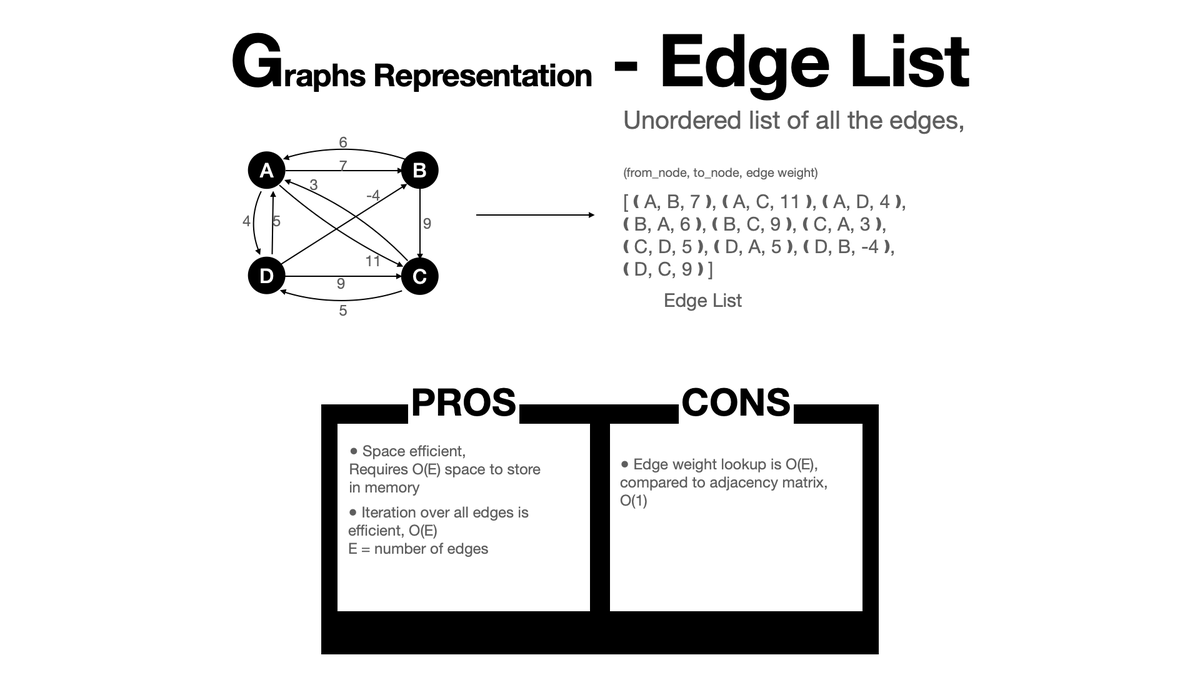
- Edge List.
An edge list is a way to represent graph simply as an unordered list of edges. Edges are represented using triplet(u,v,w), means: 'The cost from node u to node v is w'.
Thank you and see you in the next.